Michalewicz Function
Michalewicz Function
Minimize the standard Michalewicz Function, the definition of which is given below:
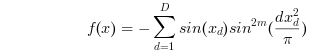
Mathematical formulation:
Minimize:
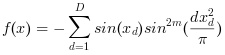
Subjected to:
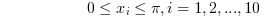
clc; function f=ObjectiveFunction(X) m = 10; nVar = length(X); d = length(X); f = 0; for n = 1:nVar f = f - sin(X(n))*((sin((n*X(n)^2)/%pi))^(2*m)); end f = -f; endfunction nVar = 2; lb = zeros(1,nVar); ub = %pi*ones(1,nVar); [xopt,fopt,exitflag,output,lambda] = fminbnd(ObjectiveFunction,lb,ub) disp (nVar) disp(fopt) disp(xopt') |
Expected Output:
Optimal Solution Found. 2. 1.165D-25 0.3075 0.3075 |
