Transportation Problem
Transportation Problem
The objective of this problem is to minimize the transportation cost of goods from the canneries to the warehouses, by satisfying the supply and demand constraints. In order to simplify the problem, it is assumed that there are two canneries and three warehouses. The supply data of canneries are as follows
| Supply (units) | |
| Cannery I | 350 |
| Cannery II | 650 |
The demands at the warehouses are as given:
| Demand (units) | |
| Warehouse A | 300 |
| Warehouse B | 300 |
| Warehouse C | 300 |
Shipping Cost between the canneries and warehouses are:
| Warehouse A (cost/unit) | Warehouse B (cost/unit) | Warehouse C (cost/unit) | |
| Cannery I | 2.5 | 1.7 | 1.8 |
| Cannery II | 2.5 | 1.8 | 1.4 |
It should be noted that, this case is solved without considering the inventory. This problem has 6 design variables and 5 linear inequality constraints. The default termination criteria of linprog solver are kept unchanged for solving this problem.
Mathematical Formulation:
Minimize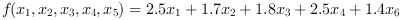
.
Subject to

clc; nCanneries = 2; nWarehouses = 3; ShippingCost = [2.5 1.7 1.8; 2.5 1.8 1.4]; demand = [300 300 300]'; supply = [350 650]'; nVar = nCanneries*nWarehouses; lb = zeros(1,nVar); // lower bounds of the amount of commodity to be shipped from each canneries to warehouses; // Linear inequality constraints // Total supply to the warehouses from a cannery should not exceed the corresponding supply limit of the same cannery for i = 1:nCanneries indeX = (i-1)*nWarehouses+1:i*nWarehouses; As(i,indeX) = ones(1,nWarehouses); end Bs = supply; As // Total supply to a warehouses from the canneries should satisfy the corresponding demand of the same warehouses //Ad = zeros() for i = 1:nWarehouses indeX = i:nWarehouses:nVar; Ad(i,indeX) = -1; end Bd = -demand; A = cat(1,As,Ad); b = cat(1,Bs,Bd); // Minimize the total transportation cost between all plants and markets Cost = zeros(nVar,1); for i = 1:nCanneries indeX = (i-1)*nWarehouses+1:i*nWarehouses; Cost(indeX) = (ShippingCost(i,:)'); end [xopt,fopt,exitflag,output,lambda] = linprog(Cost,A,b,[],[],lb,[]); // Display of results if exitflag == 0 then disp(" Optimal Solution Found") // xopt is transformed into a nCanneries X nWarehouses sized string matrix for i = 1:nCanneries indeX = (i-1)*nWarehouses+1:i*nWarehouses; X(i,1:nWarehouses) = xopt(indeX,1)'; end Values = string(X); // Labelling each markets as M_1,M_2,...,M_nWarehouses Markets(1,1) = [" "]; for j = 2:nWarehouses+1 Markets(1,j) = strcat(["M_",string(j-1)]); end // Labelling each plants as P_1,P_2,...,P_nCanneries for i = 1:nCanneries Plants(i) = strcat(["P_",string(i)]); end table = [Markets; [Plants Values]]; f = gcf(); clf as = f.axes_size; // [width height] ut = uicontrol("style","table",.. "string",table,.. "position",[150 as(2)-220 300 87]) // => @top left corner of figure // Modify by hand some values in the table. Then get them back from the ui: matrix(ut.string,size(table)) elseif exitflag == 1 then mprintf('Primal Infeasible') elseif exitflag == 2 then disp("Dual Infeasible") else disp("Technical error encountered") end |
Expected Output
Optimal Solution. Optimal Solution Found M1 M2 M3 P1 50 300 0 P2 250 0 300 |
