Product mix
Product mix problem
An engineering factory can produce five types of product (PROD 1, PROD 2,... PROD 5) by using two production processes: grinding and drilling. After deducting raw material costs, each unit of each product yields the following contributions to profit:
| Prod 1 | Prod 2 | Prod 3 | Prod 4 | Prod 5 | |
| Profit ( GBP) | 550 | 600 | 350 | 400 | 200 |
Each unit requires a certain time on each process. These are given below (in hours). A dash indicates when a process is not needed.
| Prod 1 | Prod 2 | Prod 3 | Prod 4 | Prod 5 | |
| Grinding (Hours) | 12 | 20 | - | 25 | 15 |
| Drilling (Hours) | 10 | 8 | 16 | - | - |
In addition, the final assembly of each unit of each product uses 20 hours of an employee’s time. The factory has three grinding machines and two drilling machines and works a six-day week with two shifts of 8 hours on each day. Eight workers are employed in assembly, each working one shift a day. The problem is to find how much of each product is to be manufactured so as to maximize the total profit contribution. The minimum demand for each product are as follows
| Prod 1 | Prod 2 | Prod 3 | Prod 4 | Prod 5 | |
| Demand (Units) | 5 | 5 | 2 | 7 | 2 |
The product mix problem constitutes of 5 design variables, 5 equality and 5 inequality linear constraints. In order to solve this problem the default termination criteria are used. This is an example for primal infeasible problem.
Mathematical Formulation:
Maximize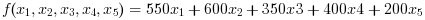
.
Subject to1. Grinding available per week

2. Drilliing capacity available per week

3. Labour capacity available per week

4. Demand for each product

clc; nProducts = 5; nMachines = [3 2]; nWorkers = 8; nDays = 6; nHours = 8; nMachineShift = 2; nWorkerShift = 1; prodProfit = [550 600 350 400 200]'; ProcessingTime = [12 20 0 25 15; 10 8 16 0 0; 20*ones(1,nProducts)]; // Linear inequalities A1 = ProcessingTime; b1 = (nDays*nHours)*[nMachines*nMachineShift nWorkers*nWorkerShift]'; // Demand constraints A2 = [-1 0 0 0 0;0 -1 0 0 0;0 0 -1 0 0; 0 0 0 -1 0; 0 0 0 0 -1]; b2 = [-5 -5 -2 -7 -2]'; A = [A1;A2]; b = [b1;b2]; lb = zeros(1,nProducts); Cost = -prodProfit; [xopt,fopt,exitflag,output,lambda]=linprog(Cost, A, b, [], [], lb,[]); // Result representation if exitflag == 0 then disp(" Optimal Solution Found") P = []; for p = 1:nProducts P = [P strcat(["PROD",string(p)])]; end disp([P;string(xopt')]); disp(["The optimal cost is ", string(fopt)]) elseif exitflag == 1 then nViolatedConstraints = sum(A*xopt-b>0) if nViolatedConstraints disp(strcat(["No of constraints violated : ", string(nViolatedConstraints)])); end elseif exitflag == 2 then disp("Dual Infeasible") else disp("Technical error encountered") end |
Expected Output:
Primal Infeasible. No of constraints violated : 2 |
