Multistage Planning

Linear Programming: Multistage Planning Problem

Reference:
Book: Applied Mathematical Programming
Author(s): Bradley, Hax and Magnanti
Publication: Addison-Wesley
Year: 1977
Chapter: 5

An automobile tire company has the ability to produce both nylon and fiberglass tires. During the next three months they have agreed to deliver tires as follows

Date	Nylon (No. of Tires)	Fiberglass (No. of Tires)
June 30	4000	1000
July 31	8000	5000
August 31	3000	5000

The company has two presses, a wheeling machine and a regal machine, and appropriate moulds that can be used to produce these tires, with the following production hours available in the upcoming months

Month	Wheeling Machine (Hours)	Regal Machine (Hours)
June	700	1500
July	300	400
August	1000	300

The production rates (hours per tire) for each machine and tire combination are as follows:

	Wheeling Machine (Hours/tire)	Regal Machine (Hours/tire)
Nylon	0.15	0.16
Fiberglass	0.12	0.14

The variable costs of producing tires are $5.00 per operating hour, regardless of which machine is being used or which tire is being produced. There is also an inventory-carrying charge of $0.10 per tire per month. How should the production be scheduled in order to meet the delivery requirements at minimum costs? This problem constitutes 16 decision variables, 6 inequality and 6 equality linear constraints. The default termination criteria for linprog solver are kept unchanged for solving this problem.

Mathematical Formulation:

The following notations are too be followed

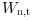= Number of nylon tires to be produced on the Wheeling machine during month t

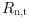= Number of nylon tires to be produced on the Regal machine during month t

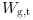= Number of fiberglass tires to be produced on the Wheeling machine in month t

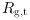= Number of fiberglass tires to be produced on the Regal machine in month t

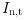= Number of nylon tires put into inventory at the end of month t

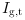= Number of fiberglass tires put into inventory at the end of month t.

Minimize

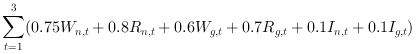Subject to

1. Capacity constraint (Production hours available)

2. Demand constraints

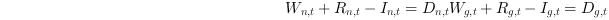
3. Non-negative constraint

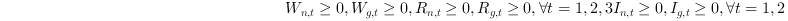
clc; 
nProducts = 2;
nMachines = 2;
nPeriods = 3;
Demand = [4000 1000;8000 5000; 3000 5000];
AvailMachineTime = [700 1500;300 400; 1000 300];
ProdRate = [0.15 0.16;0.12 0.14];
OperatingCost = 5; 
InventoryCost = 0.1;

nVar = nProducts*nMachines*nPeriods + (nPeriods-1)*nProducts; // Dimension of the problem is determined

// Linear equality constraints
// Demand constraints
nEqConstraints = nProducts*nPeriods
Aeq = zeros(nEqConstraints,nVar);
// Demand constraints for period 1
Aeq1 = zeros(nProducts,nVar);
for i = 1:nProducts
    index1 = (i-1)*nProducts+1:i*nProducts;
    Aeq1(i,index1) = 1;
    index2 = nMachines*nProducts+i;
    Aeq1(i,index2) = -1;
    beq1(i,1) = Demand(1,i);
end
// Demand constraints for period 2 to (nPeriods-1)th period
Aeq2 = zeros(nProducts,nVar);
for i = 2:nPeriods-1
    for j = 1:nProducts
        index3 = (i-1)*(nProducts*nMachines+nProducts)+(j-1)*nMachines+1:(i-1)*(nProducts*nMachines+nProducts)+(j-1)*nMachines+nMachines;
        Aeq2(j,index3) = 1; 
        index4 = (i-1)*(nProducts*nMachines+nProducts) - nProducts+j;
        Aeq2(j,index4) = 1;
        index5 = i*(nProducts*nMachines+nProducts)- nProducts+j
        Aeq2(j,index5) = -1;
        beq2(j,1) = Demand(i,j);
    end
end

// Demand constraints for last period
Aeq3 = zeros(nProducts,nVar);
for i = 1:nProducts
    index6 = (nProducts*nMachines+nProducts)*(nPeriods-1)+(i-1)*nProducts+1:(nProducts*nMachines+nProducts)*(nPeriods-1)+i*nProducts
    Aeq3(i,index6) = 1;
    index7 = (nProducts*nMachines+nProducts)*(nPeriods-1) - nProducts+i;
    Aeq3(i,index7) = 1;
    beq3(i,1) = Demand(nPeriods,i);
end
Aeq = [Aeq1;Aeq2;Aeq3];
beq = [beq1;beq2;beq3];

// Linear inequality constraints
// Machine time constraints
for i = 1:nPeriods
    for j = 1:nProducts
        Cindex = (i-1)*(nProducts*nMachines+nProducts)+j:nProducts:(i-1)*(nProducts*nMachines+nProducts)+nMachines+j;
        Rindex = (i-1)*nProducts+j;
        A(Rindex,Cindex) = ProdRate(:,j)';
        b(Rindex,1) = AvailMachineTime(i,j);
    end
end

// Objective function
TotalProductionCost = [];
for j = 1:nProducts
    TotalProductionCost = [TotalProductionCost ProdRate(j,:)*OperatingCost];
end

for i = 1:nPeriods
    index = (i-1)*(nProducts*nMachines+nProducts)+1:(i-1)*(nProducts*nMachines+nProducts)+nProducts*nMachines;
    nindex = length(index);
    cost(index,1) = TotalProductionCost';
    cost(index(nindex)+1:index(nindex)+nProducts,1) = InventoryCost;
end
cost(nVar+1:nVar+nProducts,1) = [];
lb = zeros(1,nVar);

[xopt,fopt,exitflag,output,lambda]=linprog(cost, A, b, Aeq, beq, lb,[]);

//Result representation

if exitflag == 0 then
    disp(" Optimal Solution Found")
    M = ["   "];
    for m = 1:nMachines
        M = [M strcat(["Machine",string(m)])];
    end
    P = [];
    for p = 1:nProducts
        P = [P;strcat(["Product ",string(p)])];
    end

    for i = 1:nPeriods
        Sol = [];
        for j = 1:nProducts
            Ind1 = (i-1)*(nProducts*nMachines + nProducts)+(j-1)*nProducts+1:(i-1)*(nProducts*nMachines + nProducts)+j*nProducts;
            Sol = [Sol;xopt(Ind1)']; 
        end

        disp(strcat(["Production schedule for the Period ", string(i)]));
        disp([M; [P string(Sol)]]);
    end

    for i = 1:nPeriods-1
        ind = i*(nProducts*nMachines+1:nProducts*nMachines+nProducts);
        inventory = xopt(ind);
        disp(strcat(["Inventory at the Period ", string(i)]));
        disp([P string(inventory)]);
    end

    disp(["The optimal cost is ", string(fopt)])
elseif exitflag == 1 then
    disp("Primal Infeasible")
else
    disp("Error encountered")
end

Expected Output:

Optimal Solution. Optimal Solution Found Production schedule for the Period 1 ! Machine1 Machine2 !! !!Product 1 1866.6667 7633.3333 !! !!Product 2 3500 0 ! Production schedule for the Period 2 ! Machine1 Machine2 !! !!Product 1 0 2500 !! !!Product 2 2500 0 ! Production schedule for the Period 3 ! Machine1 Machine2 !! !!Product 1 2666.6667 333.33333 !! !!Product 2 5000 0 ! Inventory at the Period 1 !Product 1 5500 !! !!Product 2 2500 ! Inventory at the Period 2 !Product 1 0 !! !!Product 2 0 ! !The optimal cost is 19173.333 !

You are here

Multistage Planning

Linear Programming: Multistage Planning Problem