Circular Tank Design problem

Design a circular tank, closed at both ends, with a volume of 200 cubic metres .The cost is proportional to the surface area of material, which is priced at $400per sqaure metre. The tank is contained within a shed with a sloping roof, thus the height of the tank h is limited by

where d is the tank diameter. Formulate the minimum cost problem and solve the design problem.

Mathematical Formulation:

Minimize: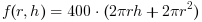

Subjected to: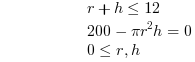

clc;

function cost=Tankprob(x)
    r = x(1);h = x(2);
    cost = (2*%pi*r*h+2*%pi*r^2)*400;
endfunction

function [ceq, c]=Nonlinearcon(x)
    r = x(1);h = x(2);
    c = [];
    ceq = 200-%pi*r^2*h;
endfunction

function y=Gradobj(x)
    y= [800*%pi*x(2) + 1600*%pi*x(1),800*%pi*x(1)];
endfunction

mprintf('\nDesign a circular tank, closed at both ends, with a volume of 200 m3 with minimum cost.\n The tank is contained within a shed with a sloping roof,thus the height of the tank h is limited')
mprintf('\nCost of material is: %f',400);
mprintf('The design variables are radius and height of the tank')

A = [1 1];b = 12;

x0 = input('Enter initial guess as vector:');
if  (sum(x0<=0) | (length(x0)~=2))
    x0 = [1 2];
    mprintf('Incorrect initial guess...\n changing initial guess to r = %d and h = %d',x0(1),x0(2));
end

lb = [0 0];
input('press enter to continue')
options=list("MaxIter",1000,"GradObj", Gradobj);

[xopt,fopt,exitflag,output1] = fmincon(Tankprob,x0,A,b,[],[],lb,[],Nonlinearcon,options);

[xopt1,fopt1,exitflag1,output2] = fmincon(Tankprob,x0,A,b,[],[],lb,[],Nonlinearcon);

clc
if exitflag == 0 then
    mprintf('Optimal Solution Found');
    mprintf('\nThe optimal radius and height of the tank are %f m and %f m',xopt(1),xopt(2));
    mprintf('\nThe volume of the tank is %f m^3',%pi*xopt(1)^2*xopt(2));
    mprintf('\nThe total surface area and cost of the tank are %f m^2 and %f $',fopt/400,fopt)
    mprintf('\nTime taken to solve the problem with gradient information is %f s and without gradient information is %f s',output1.Cpu_Time,output2.Cpu_Time);
elseif exitflag == 1 then
    mprintf('Maximum Number of Iterations Exceeded. Output may not be optimal');
    input('press enter to view results');
    printf('\nThe optimal radius and height of the tank are %f m and %f m',xopt(1),xopt(2));
    mprintf('\nThe volume of the tank is %f m^3',%pi*xopt(1)^2*xopt(2));
    mprintf('\nThe total surface area and cost of the tank are %f m^2 and %f $',fopt/400,fopt)
else
    disp("Error encountered")
end

Expected Output:

Optimal Solution Found
The optimal radiusand height of the tank are 3.169203 m and 6.338406 m
The volume of the tank is 200.000000 m^3
The total surface areaand cost of the tank are 189.322054 m^2 and 75728.821670 $
Time taken to solve the problem with gradient information is 0.181715 s and without gradient information is 0.194686 s

You are here

Circular Tank Design problem

Circular Tank Design problem