symphonymat

Solves a mixed-integer linear optimization problem (with input in Matlab format).

Calling Sequence

xopt = symphonymat(c,intcon,A,b)
xopt = symphonymat(c,intcon,A,b,Aeq,beq)
xopt = symphonymat(c,intcon,A,b,Aeq,beq,lb,ub)
xopt = symphonymat(c,intcon,A,b,Aeq,beq,lb,ub,options)
[xopt,fopt,status,output] = symphonymat( ... )

Input Parameters

c :: A vector of doubles, containing the coefficients of the variables in the objective function.
intcon :: A vector of integer constraints, specified as a vector of positive integers. The values in intcon indicate the components of the decision variable x that are integer-valued. intcon has values from 1 to n where n is the number of variable.
A :: A matrix of doubles, containing the coefficients of linear inequality constraints of size (m X n) where 'm' is the number of linear inequality constraints.
b :: A vector of doubles, related to 'A' and represents the linear coefficients in the linear inequality constraints of size (m X 1).
Aeq :: A matrix of doubles, containing the coefficients of linear equality constraints of size (m1 X n) where 'm1' is the number of linear equality constraints.
beq :: A vector of double, vector of doubles, related to 'Aeq' and represents the linear coefficients in the equality constraints of size (m1 X 1).
lb :: A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.
ub :: A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.
options :: A list, containing the option for user to specify. See below for details.

Outputs

xopt :: A vector of doubles, containing the computed solution of the optimization problem.
fopt :: A double, containing the value of the function at x.
status :: The status flag returned from symphony. See below for details.
output :: A structure, containing the information about the optimization. See below for details.

Description

Search the minimum or maximum of a constrained mixed integer linear programming optimization problem specified by :

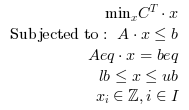
The routine calls SYMPHONY, a solver for mixed-integer linear programs written in C, for the actual computation.

Options

The options should be defined as type "list" and consist of over a hundred fields, the most important ones of which have been detailed here:

node_limit : A scalar, specifying the max. number of nodes allowed to be analyzed during the solution.
time_limit : A scalar, specifying the maximum amount of CPU time in seconds that the solver should take.
gap_limit : A scalar, representing the target gap limit allowed for solution.
granularity : A scalar, “the minimum difference between two distinct objective function values
node_selection_rule : A Scalar, specifying the maximum number of iterations that the solver should take.
prep_level : An integer, that determines the level of preprocessing that should be done on the current MILP instance.
do_branch_and_cut : A boolean, representing the decision whether to run the branch and cut algorithm or not.

The status allows the user to know the status of the optimization which is returned by Symphony. The values it can take and what they indicate is described below:

227 : Optimal Solution Found
228 : Maximum CPU Time exceeded.
229 : Maximum Number of Node Limit Exceeded.
230 : Maximum Number of Iterations Limit Exceeded.

For more details on the status, see the symphony documentation which can be found on http://www.coin-or.org/SYMPHONY/man-5.6/

The output data structure contains detailed information about the optimization process. It is of type "struct" and contains the following fields.

output.iterations: The number of iterations performed.

Example

Here we solve a simple objective function, subjected to three linear inequality constraints.

Find x in R^8 such that it minimizes:

// Example 1:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
b = [100 ,205, 249 ];
//Defining the integer constraints
intcon = [1 2 3 4];
// Calling Symphony
[x,f,status,output] = symphonymat(c,intcon,A,b)
// Press ENTER to continue

A few examples displaying the various functionalities of symphonymat have been provided below. You will find a series of problems and the appropriate code snippets to solve them.

Example

Here we build up on the previous example by adding upper and lower bounds to the variables. We add the following bounds to the problem specified above:

// Example 2:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
  c = [350*5,330*3,310*4,280*6,500,450,400,100]';
  //Inequality constraints
  A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
      1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
      1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
  b = [100 ,205, 249 ];

  // Lower Bound of variable
lb = repmat(0,1,8);
// Upper Bound of variables
ub = [repmat(1,1,4) repmat(%inf,1,4)];
  //Integer Constraints
  intcon = [1 2 3 4];
  // Calling Symphony
  [x,f,status,output] = symphonymat(c,intcon,A,b,[],[],lb,ub)
// Press ENTER to continue

Example

In this example, we proceed to add the linear equality constraints to the objective function.

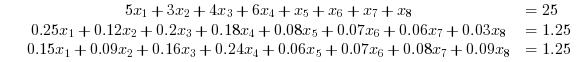
// Example 3:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
b = [100 ,205, 249 ];
// Lower Bound of variable
lb = repmat(0,1,8);
// Upper Bound of variables
ub = [repmat(1,1,4) repmat(%inf,1,4)];
// Equality Constraints
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;]
beq = [ 25, 1.25, 1.25];
  //Integer Constraints
intcon = [1 2 3 4];
// Calling Symphony
[x,f,status,output] = symphonymat(c,intcon,A,b,Aeq,beq,lb,ub)
// Press ENTER to continue

Example

In this example, we further enhance the functionality of symphonymat by setting input options. This provides us with the ability to control the solver parameters such as the maximum number of solver iterations and the max. CPU time allowed for the computation.

// Example 4:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
b = [100 ,205, 249 ];
// Lower Bound of variable
lb = repmat(0,1,8);
// Upper Bound of variables
ub = [repmat(1,1,4) repmat(%inf,1,4)];
// Equality Constraints
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;]
beq = [ 25, 1.25, 1.25];
  //Integer Constraints
intcon = [1 2 3 4];
//Options
options = list("time_limit", 25);
// Calling Symphony
[x,f,status,output] = symphonymat(c,intcon,A,b,Aeq,beq,lb,ub)
// Press ENTER to continue

Example

Primal Infeasible Problems: Find x in R^8 such that it minimizes:

Find x in R^8 such that it minimizes:

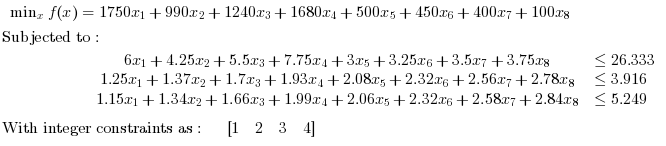
// Example 5:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer 
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints 
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ]; 
b = [26.333 ,3.916 ,5.249 ];
  //Integer Constraints
intcon = [1 2 3 4];
 
// Calling Symphony
 
[x,f,status,output] = symphonymat(c,intcon,A,b)
// Press ENTER to continue

Example

Unbounded Problems. Find x in R^8 such that it minimizes:

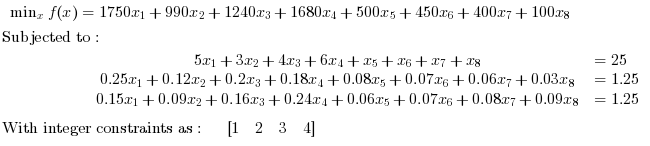
// Example 6:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints
A = [];
b = [];
// Equality Constraints
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;]
beq = [ 25, 1.25, 1.25];
  //Integer Constraints
intcon = [1 2 3 4];
// Calling Symphony
[x,f,status,output] = symphonymat(c,intcon,A,b,Aeq,beq)
// Press ENTER to continue

Authors

Keyur Joshi, Saikiran, Iswarya, Harpreet Singh

You are here

symphonymat

Calling Sequence

Input Parameters

Outputs

Description

Options

Example

Example

Example

Example

Example

Example

Authors