symphony
Solves a mixed-integer linear optimization problem.
Calling Sequence
xopt = symphony(nbVar,nbCon,c,isInt,lb,ub,A,conLB,conUB) xopt = symphony(nbVar,nbCon,c,isInt,lb,ub,A,conLB,conUB,objSense) xopt = symphony(nbVar,nbCon,c,isInt,lb,ub,A,conLB,conUB,objSense,options) [xopt,fopt,status,output] = symphony( ... )
Input Parameters
- nbVar :
A double, representing the number of variables.
- nbCon :
A double, representing the number of constraints.
- c :
A vector of doubles, representing the coefficients of the variables in the objective.
- isInt :
A vector of booleans, representing whether a variable is constrained to be an integer.
- lb :
A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.
- ub :
A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.
- A :
A matrix of double, representing the constraint matrix in conLB ≤ A⋅x ≤ conUB.
- conLB :
A vector of double, representing the lower bounds of the constraints conLB ≤ A⋅x ≤ conUB.
- conUB :
A vector of double, representing the upper bounds of the constraints conLB ≤ A⋅x ≤ conUB.
- objSense :
The sense (maximization/minimization) of the objective. Use 1(sym_minimize ) or -1 (sym_maximize) here.
- options :
A list, containing the option for user to specify. See below for details.
Outputs
- xopt :
A vector of doubles, containing the computed solution of the optimization problem.
- fopt :
A double, containing the value of the function at x.
- status :
The status flag returned from symphony. See below for details.
- output :
A structure, containing the information about the optimization. See below for details.
Description
Search the minimum or maximum of a constrained mixed integer linear programming optimization problem specified by:
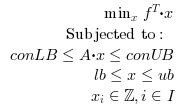
The routine calls SYMPHONY, a solver for mixed-integer linear programs written in C, for the actual computation.
Options
The options should be defined as type "list" and consist of over a hundred fields, the most important ones of which have been detailed here:- node_limit : A scalar, specifying the max. number of nodes allowed to be analyzed during the solution.
- time_limit : A scalar, specifying the maximum amount of CPU time in seconds that the solver should take.
- gap_limit : A scalar, representing the target gap limit allowed for solution.
- granularity : A scalar, “the minimum difference between two distinct objective function values
- node_selection_rule : A Scalar, specifying the maximum number of iterations that the solver should take.
- prep_level : An integer, that determines the level of preprocessing that should be done on the current MILP instance.
- do_branch_and_cut : A boolean, representing the decision whether to run the branch and cut algorithm or not.
The status allows the user to know the status of the optimization which is returned by Symphony. The values it can take and what they indicate is described below:
- 227 : Optimal Solution Found
- 228 : Maximum CPU Time exceeded.
- 229 : Maximum Number of Node Limit Exceeded.
- 230 : Maximum Number of Iterations Limit Exceeded.
For more details on the status, see the symphony documentation which can be found on http://www.coin-or.org/SYMPHONY/man-5.6/
The output data structure contains detailed information about the optimization process. It is of type "struct" and contains the following fields.
- output.iterations: The number of iterations performed.
A few examples displaying the various functionalities of symphony have been provided below. You will find a series of problems and the appropriate code snippets to solve them.
Example

//Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. // Objective function c = [350*5,330*3,310*4,280*6,500,450,400,100]'; // Lower Bound of variable lb = repmat(0,8,1); // Upper Bound of variables ub = [repmat(1,4,1);repmat(%inf,4,1)]; // Constraint Matrix A = [5,3,4,6,1,1,1,1; 5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03; 5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;] // Lower Bound of constraints conlb = [ 25; 1.25; 1.25] // Upper Bound of constraints conub = [ 25; 1.25; 1.25] // Row Matrix for telling symphony that the is integer or not isInt = [repmat(%t,1,4) repmat(%f,1,4)]; xopt = [1 1 0 1 7.25 0 0.25 3.5] fopt = [8495] options = list("time_limit", 25); // Calling Symphony [x,f,status,output] = symphony(8,3,c,isInt,lb,ub,A,conlb,conub,1,options); // Press ENTER to continue |
Example
Here we provide the sense (maximization/minimization) of the objective and show how we can further enhance the functionality of symphony by setting input options. This provides us with the ability to control the solver parameters such as the maximum number of solver iterations and the max. CPU time allowed for the computation.
//Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. // Objective function c = [350*5,330*3,310*4,280*6,500,450,400,100]'; // Lower Bound of variable lb = repmat(0,8,1); // Upper Bound of variables ub = [repmat(1,4,1);repmat(%inf,4,1)]; // Constraint Matrix A = [5,3,4,6,1,1,1,1; 5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03; 5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;] // Lower Bound of constraints conlb = [ 25; 1.25; 1.25] // Upper Bound of constraints conub = [ 25; 1.25; 1.25] // Row Matrix for telling symphony that the is integer or not isInt = [repmat(%t,1,4) repmat(%f,1,4)]; xopt = [1 1 0 1 7.25 0 0.25 3.5] fopt = [8495] options = list("time_limit", 25); // Calling Symphony [x,f,status,output] = symphony(8,3,c,isInt,lb,ub,A,conlb,conub,1,options); // Press ENTER to continue |
Example
An advanced example for Symphony.
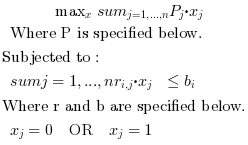
// Example 3: // This problem is taken from // P.C.Chu and J.E.Beasley // "A genetic algorithm for the multidimensional knapsack problem", // Journal of Heuristics, vol. 4, 1998, pp63-86. // The problem to be solved is: // Max sum{j=1,...,n} p(j)x(j) // st sum{j=1,...,n} r(i,j)x(j) <= b(i) i=1,...,m // x(j)=0 or 1 // The function to be maximize i.e. P(j) c = [ 504 803 667 1103 834 585 811 856 690 832 846 813 868 793 .. 825 1002 860 615 540 797 616 660 707 866 647 746 1006 608 .. 877 900 573 788 484 853 942 630 591 630 640 1169 932 1034 .. 957 798 669 625 467 1051 552 717 654 388 559 555 1104 783 .. 959 668 507 855 986 831 821 825 868 852 832 828 799 686 .. 510 671 575 740 510 675 996 636 826 1022 1140 654 909 799 .. 1162 653 814 625 599 476 767 954 906 904 649 873 565 853 1008 632]'; //Constraint Matrix A = [ //Constraint 1 42 41 523 215 819 551 69 193 582 375 367 478 162 898 .. 550 553 298 577 493 183 260 224 852 394 958 282 402 604 .. 164 308 218 61 273 772 191 117 276 877 415 873 902 465 .. 320 870 244 781 86 622 665 155 680 101 665 227 597 354 .. 597 79 162 998 849 136 112 751 735 884 71 449 266 420 .. 797 945 746 46 44 545 882 72 383 714 987 183 731 301 .. 718 91 109 567 708 507 983 808 766 615 554 282 995 946 651 298; //Constraint 2 509 883 229 569 706 639 114 727 491 481 681 948 687 941 .. 350 253 573 40 124 384 660 951 739 329 146 593 658 816 .. 638 717 779 289 430 851 937 289 159 260 930 248 656 833 .. 892 60 278 741 297 967 86 249 354 614 836 290 893 857 .. 158 869 206 504 799 758 431 580 780 788 583 641 32 653 .. 252 709 129 368 440 314 287 854 460 594 512 239 719 751 .. 708 670 269 832 137 356 960 651 398 893 407 477 552 805 881 850; //Constraint 3 806 361 199 781 596 669 957 358 259 888 319 751 275 177 .. 883 749 229 265 282 694 819 77 190 551 140 442 867 283 .. 137 359 445 58 440 192 485 744 844 969 50 833 57 877 .. 482 732 968 113 486 710 439 747 174 260 877 474 841 422 .. 280 684 330 910 791 322 404 403 519 148 948 414 894 147 .. 73 297 97 651 380 67 582 973 143 732 624 518 847 113 .. 382 97 905 398 859 4 142 110 11 213 398 173 106 331 254 447 ; //Constraint 4 404 197 817 1000 44 307 39 659 46 334 448 599 931 776 .. 263 980 807 378 278 841 700 210 542 636 388 129 203 110 .. 817 502 657 804 662 989 585 645 113 436 610 948 919 115 .. 967 13 445 449 740 592 327 167 368 335 179 909 825 614 .. 987 350 179 415 821 525 774 283 427 275 659 392 73 896 .. 68 982 697 421 246 672 649 731 191 514 983 886 95 846 .. 689 206 417 14 735 267 822 977 302 687 118 990 323 993 525 322; //Constrain 5 475 36 287 577 45 700 803 654 196 844 657 387 518 143 .. 515 335 942 701 332 803 265 922 908 139 995 845 487 100 .. 447 653 649 738 424 475 425 926 795 47 136 801 904 740 .. 768 460 76 660 500 915 897 25 716 557 72 696 653 933 .. 420 582 810 861 758 647 237 631 271 91 75 756 409 440 .. 483 336 765 637 981 980 202 35 594 689 602 76 767 693 .. 893 160 785 311 417 748 375 362 617 553 474 915 457 261 350 635 ; ]; nbCon = size(A,1) nbVar = size(A,2) // Lower Bound of variables lb = repmat(0,nbVar,1) // Upper Bound of variables ub = repmat(1,nbVar,1) // Row Matrix for telling symphony that the is integer or not isInt = repmat(%t,1,nbVar) // Lower Bound of constraints conLB=repmat(0,nbCon,1); // Upper Bound of constraints conUB=[11927 13727 11551 13056 13460 ]'; options = list("time_limit", 25); // The expected solution : // Output variables xopt = [0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 .. 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 .. 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 1 0 0 1 0] // Optimal value fopt = [ -24381 ] // Calling Symphony [x,f,status,output] = symphony(nbVar,nbCon,c,isInt,lb,ub,A,conLB,conUB,-1,options); |
Authors
- Keyur Joshi, Saikiran, Iswarya, Harpreet Singh
