Input Parameters

fun :

A function, representing the objective function and gradient (if given) of the problem.

x0 :

A vector of doubles, containing the starting values of variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

lb :

A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

ub :

A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

options :

A list, containing the option for user to specify. See below for details.

Outputs

xopt :

A vector of doubles, containing the computed solution of the optimization problem.

resnorm :

A double, containing the objective value returned as a scalar value i.e. sum(fun(x).^2).

residual :

A vector of doubles, containing the solution of the objective function, returned as a vector i.e. fun(x).

exitflag :

An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.

output :

A structure, containing the information about the optimization. See below for details.

lambda :

A structure, containing the Lagrange multipliers of the lower bounds, upper bounds and constraints at the optimized point. See below for details.

gradient :

A vector of doubles, containing the objective's gradient of the solution.

Description

Search the minimum of a constrained nonlinear least square problem specified by :

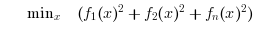
lsqnonlin calls fmincon, which calls Ipopt, an optimization library written in C++ to solve the nonlinear least squares problem.

The options should be defined as type "list" and consist of the following fields:

options= list("MaxIter", [---], "CpuTime", [---], "GradObj", ---);

• MaxIter : A Scalar, specifying the maximum number of iterations that the solver should take.
• CpuTime : A Scalar, specifying the maximum amount of CPU time in seconds that the solver should take.
• GradObj : A string, representing whetherthe gradient function is on or off.

The default values for the various items are given as:

Default Values : options = list("MaxIter", [3000], "CpuTime", [600], "GradObj", "off");

The exitflag allows the user to know the status of the optimization which is returned by Ipopt. The values it can take and what they indicate is described below:

• 0 : Optimal Solution Found
• 1 : Maximum Number of Iterations Exceeded. Output may not be optimal.
• 2 : Maximum amount of CPU Time exceeded. Output may not be optimal.
• 3 : Stop at Tiny Step.
• 4 : Solved To Acceptable Level.
• 5 : Converged to a point of local infeasibility.

For more details on exitflag, see the Ipopt documentation which can be found on http://www.coin-or.org/Ipopt/documentation/

The output data structure contains detailed information about the optimization process. It is of type "struct" and contains the following fields.

• output.iterations: The number of iterations performed.
• output.constrviolation: The max-norm of the constraint violation.

The lambda data structure contains the Lagrange multipliers at the end of optimization. In the current version, the values are returned only when the the solution is optimal. It has type "struct" and contains the following fields.

• lambda.lower: The Lagrange multipliers for the lower bound constraints.
• lambda.upper: The Lagrange multipliers for the upper bound constraints.

Example

Here we solve a simple nonlinear least square example taken from leastsq default present in scilab.

Find x in R^2 such that it minimizes:

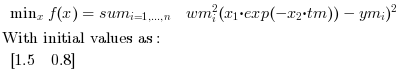
// we have the m measures (ti, yi): m = 10; tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]'; ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]'; // measure weights (here all equal to 1...) wm = ones(m,1); // and we want to find the parameters x such that the model fits the given // data in the least square sense: // // minimize f(x) = sum_i wm(i)^2 ( x(1)*exp(-x(2)*tm(i) - ym(i) )^2 // initial parameters guess x0 = [1.5 ; 0.8]; // in the first examples, we define the function fun and dfun // in scilab language function y=myfun(x, them, ym, wm) y = wm.*( x(1)*exp(-x(2)*tm) - ym ) endfunction // the simplest call [xopt,resnorm,residual,exitflag,output,lambda,gradient] = lsqnonlin(myfun,x0) // Press ENTER to continue

Example

Here we build up on the previous example by adding upper and lower bounds to the variables. We add the following bounds to the problem specified above:

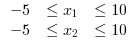
//A simple nonlinear least square example taken from leastsq default present in scilab function y=yth(t, x) y = x(1)*exp(-x(2)*t) endfunction // we have the m measures (ti, yi): m = 10; tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]'; ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]'; // measure weights (here all equal to 1...) wm = ones(m,1); // and we want to find the parameters x such that the model fits the given // data in the least square sense: // // minimize f(x) = sum_i wm(i)^2 ( yth(tm(i),x) - ym(i) )^2 // initial parameters guess x0 = [1.5 ; 0.8]; // in the first examples, we define the function fun and dfun // in scilab language function y=myfun(x, tm, ym, wm) y = wm.*( yth(tm, x) - ym ) endfunction lb = [-5 ,-5]; ub = [10, 10]; // the simplest call [xopt,resnorm,residual,exitflag,output,lambda,gradient] = lsqnonlin(myfun,x0,lb,ub) // Press ENTER to continue

Example

In this example, we further enhance the functionality of lsqnonlin by setting input options. This provides us with the ability to control the solver parameters such as the maximum number of solver iterations and the max. CPU time allowed for the computation.

//A basic example taken from leastsq default present in scilab with gradient function y=yth(t, x) y = x(1)*exp(-x(2)*t) endfunction // we have the m measures (ti, yi): m = 10; tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]'; ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]'; // measure weights (here all equal to 1...) wm = ones(m,1); // and we want to find the parameters x such that the model fits the given // data in the least square sense: // // minimize f(x) = sum_i wm(i)^2 ( yth(tm(i),x) - ym(i) )^2 // initial parameters guess x0 = [1.5 ; 0.8]; // in the first examples, we define the function fun and dfun // in scilab language function [y, dy]=myfun(x, tm, ym, wm) y = wm.*( x(1)*exp(-x(2)*tm) - ym ) v = wm.*exp(-x(2)*tm) dy = [v , -x(1)*tm.*v] endfunction lb = [-5,-5]; ub = [10,10]; options = list("GradObj", "on") [xopt,resnorm,residual,exitflag,output,lambda,gradient] = lsqnonlin(myfun,x0,lb,ub,options)

Authors

• Harpreet Singh