Input Parameters

H :

A symmetric matrix of doubles, representing the Hessian of the quadratic problem.

f :

A vector of doubles, representing coefficients of the linear terms in the quadratic problem.

intcon :

A vector of integers, representing the variables that are constrained to be integers.

A :

A matrix of doubles, containing the coefficients of linear inequality constraints of size (m X n) where 'm' is the number of linear inequality constraints.

b :

A vector of doubles, related to 'A' and represents the linear coefficients in the linear inequality constraints of size (m X 1).

Aeq :

A matrix of doubles, containing the coefficients of linear equality constraints of size (m1 X n) where 'm1' is the number of linear equality constraints.

beq :

A vector of double, vector of doubles, related to 'Aeq' and represents the linear coefficients in the equality constraints of size (m1 X 1).

lb :

A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

ub :

A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

x0 :

A vector of doubles, containing the starting values of variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

options :

A list, containing the option for user to specify. See below for details.

file_path :

path to bonmin opt file if used.

Outputs

xopt :

A vector of doubles, containing the computed solution of the optimization problem.

fopt :

A double, containing the value of the function at xopt.

exitflag :

An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.

output :

A structure, containing the information about the optimization. See below for details.

Description

Search the minimum of a constrained linear quadratic optimization problem specified by :

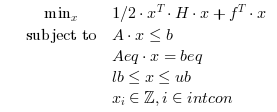
intquadprog calls Bonmin, a library written in C++ to solve the quadratic problem.

The exitflag allows to know the status of the optimization which is given back by Ipopt.

• 0 : Optimal Solution Found
• 1 : InFeasible Solution.
• 2 : Objective Function is Continuous Unbounded.
• 3 : Limit Exceeded.
• 4 : User Interrupt.
• 5 : MINLP Error.

For more details on exitflag, see the Bonmin documentation which can be found on http://www.coin-or.org/Bonmin

The output data structure contains detailed information about the optimization process. It is of type "struct" and contains the following fields.

• output.constrviolation: The max-norm of the constraint violation.

Example

Here we solve a simple objective function.

Find x in R^6 such that it minimizes:

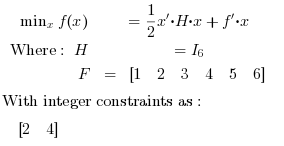
//Example 1:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon)

Example

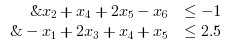
//Example 2:
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b)

Example

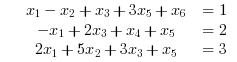
//Example 3:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Equality constraints
Aeq= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6;
2,5,3,0,1,0];
beq=[1; 2; 3];
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b,Aeq,beq)

Example

In this example, we proceed to add the upper and lower bounds to the objective function.

//Example 4:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Equality constraints
Aeq= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6;
2,5,3,0,1,0];
beq=[1; 2; 3];
//Variable bounds
lb=[-1000; -10000; 0; -1000; -1000; -1000];
ub=[10000; 100; 1.5; 100; 100; 1000];
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b,Aeq,beq,lb,ub)

Example

In this example, we initialize the values of x to speed up the computation. We further enhance the functionality of qpipoptmat by setting input options.

//Example 5:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Equality constraints
Aeq= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6;
2,5,3,0,1,0];
beq=[1; 2; 3];
//Variable bounds
lb=[-1000; -10000; 0; -1000; -1000; -1000];
ub=[10000; 100; 1.5; 100; 100; 1000];
//Initial guess and options
x0 = repmat(0,6,1);
options = list("MaxIter", 300, "CpuTime", 100);
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b,Aeq,beq,lb,ub,x0,options)

Example

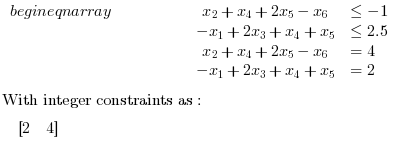
//Example 6:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6);
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Equality constraints
Aeq= [0,1,0,1,2,-1;
-1,0,-3,-4,5,6];
beq=[4; 2];
//Integer Constraints
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b,Aeq,beq)

Example

Unbounded Problems: Find x in R^6 such that it minimizes the objective function used above under the following constraints:

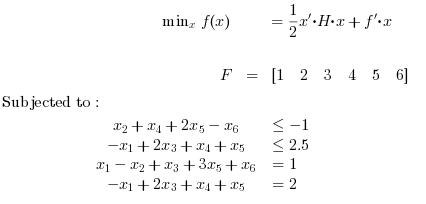
//Example 7:
//Minimize 0.5*x'*H*x + f'*x with
f=[1; 2; 3; 4; 5; 6]; H=eye(6,6); H(1,1) = -1;
//Inequality constraints
A= [0,1,0,1,2,-1;
-1,0,2,1,1,0];
b = [-1; 2.5];
//Equality constraints
Aeq= [1,-1,1,0,3,1;
-1,0,-3,-4,5,6];
beq=[1; 2];
intcon = [2 ,4];
//Running intquadprog
[xopt,fopt,exitflag,output]=intquadprog(H,f,intcon,A,b,Aeq,beq)

Authors

• Akshay Miterani and Pranav Deshpande