Input Parameters

c :

a vector of double, contains coefficients of the variables in the objective

intcon :

Vector of integer constraints, specified as a vector of positive integers. The values in intcon indicate the components of the decision variable x that are integer-valued. intcon has values from 1 through number of variable.

A :

A matrix of doubles, containing the coefficients of linear inequality constraints of size (m X n) where 'm' is the number of linear inequality constraints.

b :

A vector of doubles, related to 'A' and containing the the Right hand side equation of the linear inequality constraints of size (m X 1).

Aeq :

A matrix of doubles, containing the coefficients of linear equality constraints of size (m1 X n) where 'm1' is the number of linear equality constraints.

beq :

A vector of doubles, related to 'Aeq' and containing the the Right hand side equation of the linear equality constraints of size (m1 X 1).

lb :

A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

ub :

A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

options :

A list, containing the option for user to specify. See below for details.

Outputs

xopt :

A vector of doubles, containing the computed solution of the optimization problem.

fopt :

A double, containing the the function value at x.

status :

An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.

output :

A structure, containing the information about the optimization. See below for details.

Description

Search the minimum or maximum of a constrained mixed integer linear programming optimization problem specified by :

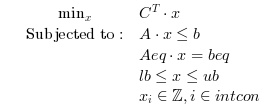
CBC, an optimization library written in C++, is used for solving the linear programming problems.

Options

options= list("IntegerTolerance", [---], "MaxNodes",[---], "MaxIter", [---], "AllowableGap",[---] "CpuTime", [---],"gradobj", "off", "hessian", "off" );

• IntegerTolerance : A Scalar, a number with that value of an integer is considered integer.
• MaxNodes : A Scalar, containing the maximum number of nodes that the solver should search.
• MaxTime : A scalar, specifying the maximum amount of CPU Time in seconds that the solver should take.
• AllowableGap : A scalar, that specifies the gap between the computed solution and the the objective value of the best known solution stop, at which the tree search can be stopped.

options = list('integertolerance',1d-06,'maxnodes',2147483647,'cputime',1d10,'allowablegap')

The exitflag allows the user to know the status of the optimization which is returned by OSI-CBC. The values it can take and what they indicate is described below:

• 0 : Optimal Solution Found
• 1 : Converged to a point of primal infeasibility.
• 2 : Solution Limit is reached
• 3 : Node Limit is reached. Output may not be optimal.
• 4 : Numerical Difficulties.
• 5 : Maximum amount of CPU Time exceeded.
• 6 : Continuous Solution Unbounded.
• 7 : Converged to a point of dual infeasibility.

For more details on exitflag, see the Bonmin documentation which can be found on http://www.coin-or.org/Cbc

Example

Here we solve a simple objective function, subjected to three linear inequality constraints.

Find x in R^8 such that it minimizes:

// Example 1:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
b = [100 ,205, 249 ];
//Defining the integer constraints
intcon = [1 2 3 4];
// Calling Symphony
[x,f,status,output] = intlinprog(c,intcon,A,b)
// Press ENTER to continue

Example

Here we build up on the previous example by adding upper and lower bounds to the variables. We add the following bounds to the problem specified above:

// Example 2:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
  c = [350*5,330*3,310*4,280*6,500,450,400,100]';
  //Inequality constraints
  A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
      1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
      1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
  b = [100 ,205, 249 ];
  // Lower Bound of variable
lb = repmat(0,1,8);
// Upper Bound of variables
ub = [repmat(1,1,4) repmat(%inf,1,4)];
  //Integer Constraints
  intcon = [1 2 3 4];
  // Calling Symphony
  [x,f,status,output] = intlinprog(c,intcon,A,b,[],[],lb,ub)
// Press ENTER to continue

Example

In this example, we proceed to add the linear equality constraints to the objective function.

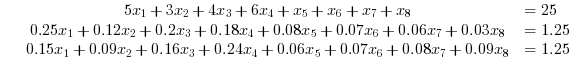
// Example 3:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ];
b = [100 ,205, 249 ];
// Lower Bound of variable
lb = repmat(0,1,8);
// Upper Bound of variables
ub = [repmat(1,1,4) repmat(%inf,1,4)];
// Equality Constraints
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;]
beq = [ 25, 1.25, 1.25];
  //Integer Constraints
intcon = [1 2 3 4];
// Calling CBC
[x,f,status,output] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
// Press ENTER to continue

Example

Primal Infeasible Problems: Find x in R^8 such that it minimizes:

Find x in R^8 such that it minimizes:

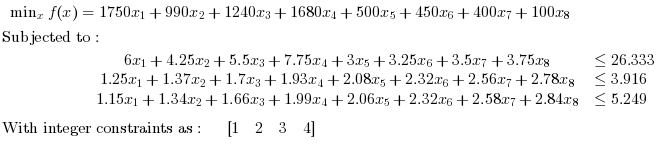
// Example 4:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer 
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints 
A = [6,4.25, 5.5, 7.75, 3, 3.25, 3.5,3.75; 
    1.25,1.37,1.7,1.93,2.08,2.32,2.56,2.78;  
    1.15,1.34,1.66,1.99,2.06,2.32,2.58,2.84 ]; 
b = [26.333 ,3.916 ,5.249 ];
  //Integer Constraints
intcon = [1 2 3 4];
 
// Calling CBC
 
[x,f,status,output] = intlinprog(c,intcon,A,b)
// Press ENTER to continue

Example

Unbounded Problems. Find x in R^8 such that it minimizes:

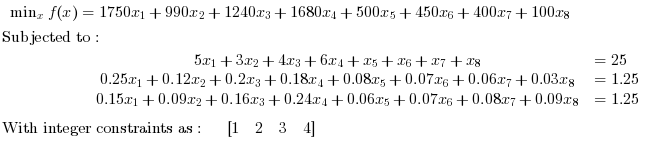
// Example 5:
// Reference: Westerberg, Carl-Henrik, Bengt Bjorklund, and Eskil Hultman. "An application of mixed integer
// programming in a Swedish steel mill." Interfaces 7, no. 2 (1977): 39-43. Modified acc. to requirements.
c = [350*5,330*3,310*4,280*6,500,450,400,100]';
//Inequality constraints
A = [];
b = [];
// Equality Constraints
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09;]
beq = [ 25, 1.25, 1.25];
  //Integer Constraints
intcon = [1 2 3 4];
// Calling CBC
[x,f,status,output] = intlinprog(c,intcon,A,b,Aeq,beq)
// Press ENTER to continue

Authors

• Akshay Miterani and Pranav Deshpande