intfminimax

Solves a mixed-integer minimax optimization problem.

Calling Sequence

xopt = intfminimax(fun,x0,intcon)
xopt = intfminimax(fun,x0,intcon,A,b)
xopt = intfminimax(fun,x0,intcon,A,b,Aeq,beq)
xopt = intfminimax(fun,x0,intcon,A,b,Aeq,beq,lb,ub)
xopt = intfminimax(fun,x0,intcon,A,b,Aeq,beq,lb,ub,nonlinfun)
xopt = intfminimax(fun,x0,intcon,A,b,Aeq,beq,lb,ub,nonlinfun,options)
[xopt, fval] = intfminimax(.....)
[xopt, fval, maxfval]= intfminimax(.....)
[xopt, fval, maxfval, exitflag]= intfminimax(.....)

Input Parameters

fun:

The function to be minimized. fun is a function that has a vector x as an input argument, and contains the objective functions evaluated at x.

x0 :

A vector of doubles, containing the starting values of variables of size (1 X n) or (n X 1) where 'n' is the number of Variables.

A :

A matrix of doubles, containing the coefficients of linear inequality constraints of size (m X n) where 'm' is the number of linear inequality constraints.

b :

A vector of doubles, related to 'A' and represents the linear coefficients in the linear inequality constraints of size (m X 1).

Aeq :

A matrix of doubles, containing the coefficients of linear equality constraints of size (m1 X n) where 'm1' is the number of linear equality constraints.

beq :

A vector of double, vector of doubles, related to 'Aeq' and represents the linear coefficients in the equality constraints of size (m1 X 1).

intcon :

A vector of integers, representing the variables that are constrained to be integers.

lb :

A vector of doubles, containing the lower bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

ub :

A vector of doubles, containing the upper bounds of the variables of size (1 X n) or (n X 1) where 'n' is the number of variables.

nonlinfun:

A function, representing the nonlinear Constraints functions(both Equality and Inequality) of the problem. It is declared in such a way that nonlinear inequality constraints (c), and the nonlinear equality constraints (ceq) are defined as separate single row vectors.

options :

A list, containing the option for user to specify. See below for details.

Outputs

xopt :

A vector of doubles, containing the computed solution of the optimization problem.

fopt :

A vector of doubles, containing the values of the objective functions at the end of the optimization problem.

maxfval:

A double, representing the maximum value in the vector fval.

exitflag :

An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.

output :

A structure, containing the information about the optimization. See below for details.

lambda :

A structure, containing the Lagrange multipliers of lower bound, upper bound and constraints at the optimized point. See below for details.

Description

intfminimax minimizes the worst-case (largest) value of a set of multivariable functions, starting at an initial estimate. This is generally referred to as the minimax problem.

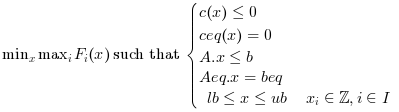
max-min problems can also be solved with intfminimax, using the identity

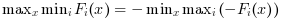
Currently, intfminimax calls intfmincon, which uses the bonmin algorithm, an optimization library in C++.

Options

The options allow the user to set various parameters of the Optimization problem. The syntax for the options is given by:

options= list("IntegerTolerance", [---], "MaxNodes",[---], "MaxIter", [---], "AllowableGap",[---] "CpuTime", [---],"gradobj", "off", "hessian", "off" );

  • IntegerTolerance : A Scalar, a number with that value of an integer is considered integer.
  • MaxNodes : A Scalar, containing the maximum number of nodes that the solver should search.
  • CpuTime : A scalar, specifying the maximum amount of CPU Time in seconds that the solver should take.
  • AllowableGap : A scalar, that specifies the gap between the computed solution and the the objective value of the best known solution stop, at which the tree search can be stopped.
  • MaxIter : A scalar, specifying the maximum number of iterations that the solver should take.
  • gradobj : A string, to turn on or off the user supplied objective gradient.
  • hessian : A scalar, to turn on or off the user supplied objective hessian.
The default values for the various items are given as:

options = list('integertolerance',1d-06,'maxnodes',2147483647,'cputime',1d10,'allowablegap',0,'maxiter',2147483647,'gradobj',"off",'hessian',"off")

The objective function must have header :

F = fun(x)
where x is a n x 1 matrix of doubles and F is a m x 1 matrix of doubles where m is the total number of objective functions inside F. On input, the variable x contains the current point and, on output, the variable F must contain the objective function values.

By default, the gradient options for intfminimax are turned off and and fmincon does the gradient opproximation of minmaxObjfun. In case the GradObj option is off and GradCon option is on, intfminimax approximates minmaxObjfun gradient using the numderivative toolbox.

If we can provide exact gradients, we should do so since it improves the convergence speed of the optimization algorithm.

The exitflag allows to know the status of the optimization which is given back by Bonmin.

  • 0 : Optimal Solution Found
  • 1 : InFeasible Solution.
  • 2 : Objective Function is Continuous Unbounded.
  • 3 : Limit Exceeded.
  • 4 : User Interrupt.
  • 5 : MINLP Error.

For more details on exitflag, see the Bonmin documentation which can be found on http://www.coin-or.org/Bonmin

A few examples displaying the various functionalities of intfminimax have been provided below. You will find a series of problems and the appropriate code snippets to solve them.

Example

Here we solve a simple objective function, subjected to no constraints.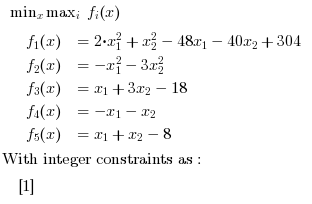

// Example 1:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
// The expected solution : only 4 digits are guaranteed
xopt = [4 4]
fopt = [0 -64 -2 -8 0]
intcon = [1]
maxfopt = 0
// Run intfminimax
[x,fval,maxfval,exitflag] = intfminimax(myfun, x0,intcon)
// Press ENTER to continue

Example

We proceed to add simple linear inequality constraints.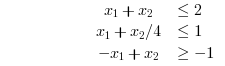

//Example 2:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
//Linear Inequality constraints
A=[1,1 ; 1,1/4 ; 1,-1];
b=[2;1;1];
////Integer constraints
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output,lambda] = intfminimax(myfun, intcon,x0,A,b)

Example

Here we build up on the previous example by adding linear equality constraints. We add the following constraints to the problem specified above: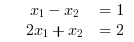

//Example 3:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
//Linear Inequality constraints
A=[1,1 ; 1,1/4 ; 1,-1];
b=[2;1;1];
//We specify the linear equality constraints below.
Aeq = [1,-1; 2, 1];
beq =  [1;2];
//Integer constraints
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output,lambda] = intfminimax(myfun, intcon,x0,A,b,Aeq,beq)

Example

In this example, we proceed to add the upper and lower bounds to the objective function.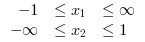

//Example 4:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
//Linear Inequality constraints
A=[1,1 ; 1,1/4 ; 1,-1];
b=[2;1;1];
//We specify the linear equality constraints below.
Aeq = [1,-1; 2, 1];
beq =  [1;2];
//The upper and lower bounds for the objective function are defined in simple vectors as shown below.
lb = [-1;-%inf];
ub = [%inf;1];    
//Integer constraints
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output,lambda] = intfminimax(myfun, intcon,x0,A,b,Aeq,beq,lb,ub)

Example

Finally, we add the nonlinear constraints to the problem. Note that there is a notable difference in the way this is done as compared to defining the linear constraints.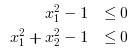

//Example 5:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
//Linear Inequality constraints
A=[1,1 ; 1,1/4 ; 1,-1];
b=[2;1;1];
//We specify the linear equality constraints below.
Aeq = [1,-1; 2, 1];
beq =  [1;2];
//The upper and lower bounds for the objective function are defined in simple vectors as shown below.
lb = [-1;-%inf];
ub = [%inf;1];    //
//Nonlinear constraints are required to be defined as a single function with the inequality and equality constraints in separate vectors.
function [c, ceq]=nlc(x)
c=[x(1)^2-1,x(1)^2+x(2)^2-1];
ceq=[];
endfunction
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output,lambda] = intfminimax(myfun, intcon,x0,A,b,Aeq,beq,lb,ub)

Example

We can further enhance the functionality of fminimax by setting input options. We can pre-define the gradient of the objective function and/or the hessian of the lagrange function and thereby improve the speed of computation. This is elaborated on in example 6. We take the following problem, specify the gradients, and the jacobian matrix of the constraints. We also set solver parameters using the options.

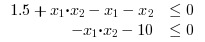
//Example 6: Using the available options
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction

// Defining gradient of myfun
function G=myfungrad(x)
G = [ 4*x(1) - 48, -2*x(1), 1, -1, 1;
2*x(2) - 40, -6*x(2), 3, -1, 1; ]'
endfunction
// The nonlinear constraints and the Jacobian
// matrix of the constraints
function [c, ceq]=confun(x)
// Inequality constraints
c = [1.5 + x(1)*x(2) - x(1) - x(2), -x(1)*x(2) - 10]
// No nonlinear equality constraints
ceq=[]
endfunction
// Defining gradient of confungrad
function [DC, DCeq]=cgrad(x)
// DC(:,i) = gradient of the i-th constraint
// DC = [
//   Dc1/Dx1  Dc1/Dx2
//   Dc2/Dx1  Dc2/Dx2
//   ]
DC= [
x(2)-1, -x(2)
x(1)-1, -x(1)
]'
DCeq = []'
endfunction
// Test with both gradient of objective and gradient of constraints
Options = list("MaxIter", [3000], "CpuTime", [600],"GradObj",myfungrad,"GradCon",cgrad);
// The initial guess
x0 = [0,10];
// The expected solution : only 4 digits are guaranteed
xopt = [0.92791 7.93551]
fopt = [6.73443  -189.778  6.73443  -8.86342  0.86342]
maxfopt = 6.73443
//integer constraints
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output] = intfminimax(myfun,intcon,x0,[],[],[],[],[],[], confun, Options)

Example

Infeasible Problems: Find x in R^2 such that it minimizes the objective function used above under the following constraints: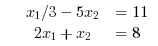

//Example 7:
//Objective function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
//Linear Inequality constraints
A=[1,1 ; 1,1/4 ; 1,-1];
b=[2;1;1];
//We specify the linear equality constraints below.
Aeq = [1/3,-5; 2, 1];
beq =  [11;8];
//integer constraints
intcon = [1];
// Run intfminimax
[x,fval,maxfval,exitflag,output,lambda] = intfminimax(myfun,intcon, x0,A,b,Aeq,beq)

Authors

  • Harpreet Singh