Input Parameters

f :

A function, representing the objective function of the problem.

x0 :

A vector of doubles, containing the starting values of variables of size (1 X n) or (n X 1) where 'n' is the number of Variables.

options :

A list, containing the options for user to specify. See below for details.

Outputs

xopt :

A vector of doubles, containing the computed solution of the optimization problem.

fopt :

A double, containing the the function value at x.

exitflag :

An integer, containing the flag which denotes the reason for termination of algorithm. See below for details.

output :

A structure, containing the information about the optimization. See below for details.

gradient :

A vector of doubles, containing the objective's gradient of the solution.

hessian :

A matrix of doubles, containing the lagrangian's hessian of the solution.

Description

Search the minimum of an unconstrained optimization problem specified by :

Find the minimum of f(x) such that

Fminunc calls Ipopt which is an optimization library written in C++, to solve the unconstrained optimization problem.

Options

options= list("MaxIter", [---], "CpuTime", [---], "GradObj", ---, "Hessian", ---, "GradCon", ---);

• MaxIter : A Scalar, specifying the Maximum Number of Iterations that the solver should take.
• CpuTime : A Scalar, specifying the Maximum amount of CPU Time in seconds that the solver should take.
• Gradient: A function, representing the gradient function of the objective in Vector Form.
• Hessian : A function, representing the hessian function of the lagrange in the form of a Symmetric Matrix with input parameters as x, objective factor and lambda. Refer to Example 5 for definition of lagrangian hessian function.

options = list("MaxIter", [3000], "CpuTime", [600]);

The exitflag allows the user to know the status of the optimization which is returned by Ipopt. The values it can take and what they indicate is described below:

• 0 : Optimal Solution Found
• 1 : Maximum Number of Iterations Exceeded. Output may not be optimal.
• 2 : Maximum amount of CPU Time exceeded. Output may not be optimal.
• 3 : Stop at Tiny Step.
• 4 : Solved To Acceptable Level.
• 5 : Converged to a point of local infeasibility.

For more details on exitflag, see the Ipopt documentation which can be found on http://www.coin-or.org/Ipopt/documentation/

The output data structure contains detailed information about the optimization process. It is of type "struct" and contains the following fields.

• output.Iterations: The number of iterations performed.
• output.Cpu_Time : The total cpu-time taken.
• output.Objective_Evaluation: The number of objective evaluations performed.
• output.Dual_Infeasibility : The Dual Infeasiblity of the final soution.
• output.Message: The output message for the problem.

Example

We begin with the minimization of a simple non-linear function.

Find x in R^2 such that it minimizes:

//Example 1: Simple non-linear function.
//Objective function to be minimised
function y=f(x)
y= x(1)^2 + x(2)^2;
endfunction
//Starting point
x0=[2,1];
//Calling Ipopt
[xopt,fopt]=fminunc(f,x0)
// Press ENTER to continue

Example

We now look at the Rosenbrock function, a non-convex performance test problem for optimization routines. We use this example to illustrate how we can enhance the functionality of fminunc by setting input options. We can pre-define the gradient of the objective function and/or the hessian of the lagrange function and thereby improve the speed of computation. This is elaborated on in example 2. We also set solver parameters using the options.

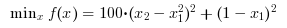
//Example 2: The Rosenbrock function.
//Objective function to be minimised
function y=f(x)
y= 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;
endfunction
//Starting point
x0=[-1,2];
//Gradient of objective function
function y=fGrad(x)
y= [-400*x(1)*x(2) + 400*x(1)^3 + 2*x(1)-2, 200*(x(2)-x(1)^2)];
endfunction
//Hessian of Objective Function
function y=fHess(x)
y= [1200*x(1)^2- 400*x(2) + 2, -400*x(1);-400*x(1), 200 ];
endfunction
//Options
options=list("MaxIter", [1500], "CpuTime", [500], "GradObj", fGrad, "Hessian", fHess);
//Calling Ipopt
[xopt,fopt,exitflag,output,gradient,hessian]=fminunc(f,x0,options)
// Press ENTER to continue

Example

Unbounded Problems: Find x in R^2 such that it minimizes:

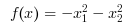
//Example 3: Unbounded objective function.
//Objective function to be minimised
function y=f(x)
y= -x(1)^2 - x(2)^2;
endfunction
//Starting point
x0=[2,1];
//Gradient of objective function
function y=fGrad(x)
y= [-2*x(1),-2*x(2)];
endfunction
//Hessian of Objective Function
function y=fHess(x)
y= [-2,0;0,-2];
endfunction
//Options
options=list("MaxIter", [1500], "CpuTime", [500], "GradObj", fGrad, "Hessian", fHess);
//Calling Ipopt
[xopt,fopt,exitflag,output,gradient,hessian]=fminunc(f,x0,options)

Authors

• R.Vidyadhar , Vignesh Kannan