fminimax Solves minimax constraint problem

Calling Sequence

xopt = fminimax(fun,x0)
xopt = fminimax(fun,x0,A,b)
xopt = fminimax(fun,x0,A,b,Aeq,beq)
xopt = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)
xopt = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlinfun)
xopt = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlinfun,options)
[xopt, fval] = fmincon(.....)
[xopt, fval, maxfval]= fmincon(.....)
[xopt, fval, maxfval, exitflag]= fmincon(.....)
[xopt, fval, maxfval, exitflag, output]= fmincon(.....)
[xopt, fval, maxfval, exitflag, output, lambda]= fmincon(.....)

Parameters

fun:

The function to be minimized. fun is a function that accepts a vector x and returns a vector F, the objective functions evaluated at x.

x0 :

a vector of double, contains initial guess of variables.

A :

a matrix of double, represents the linear coefficients in the inequality constraints A⋅x ≤ b.

b :

a vector of double, represents the linear coefficients in the inequality constraints A⋅x ≤ b.

Aeq :

a matrix of double, represents the linear coefficients in the equality constraints Aeq⋅x = beq.

beq :

a vector of double, represents the linear coefficients in the equality constraints Aeq⋅x = beq.

lb :

a vector of double, contains lower bounds of the variables.

ub :

a vector of double, contains upper bounds of the variables.

nonlinfun:

function that computes the nonlinear inequality constraints c⋅x ≤ 0 and nonlinear equality constraints c⋅x = 0.

xopt :

a vector of double, the computed solution of the optimization problem.

fopt :

a double, the value of the function at x.

maxfval:

a 1x1 matrix of doubles, the maximum value in vector fval

exitflag :

The exit status. See below for details.

output :

The structure consist of statistics about the optimization. See below for details.

lambda :

The structure consist of the Lagrange multipliers at the solution of problem. See below for details.

Description

fminimax minimizes the worst-case (largest) value of a set of multivariable functions, starting at an initial estimate. This is generally referred to as the minimax problem.

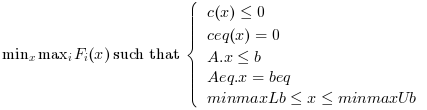
Currently, fminimax calls fmincon which uses the ip-opt algorithm.

max-min problems can also be solved with fminimax, using the identity

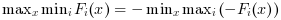
The options allows the user to set various parameters of the Optimization problem. It should be defined as type "list" and contains the following fields.

  • Syntax : options= list("MaxIter", [---], "CpuTime", [---], "GradObj", ---, "GradCon", ---);
  • MaxIter : a Scalar, containing the Maximum Number of Iteration that the solver should take.
  • CpuTime : a Scalar, containing the Maximum amount of CPU Time that the solver should take.
  • GradObj : a function, representing the gradient function of the Objective in Vector Form.
  • GradCon : a function, representing the gradient of the Non-Linear Constraints (both Equality and Inequality) of the problem. It is declared in such a way that gradient of non-linear inequality constraints are defined first as a separate Matrix (cg of size m2 X n or as an empty), followed by gradient of non-linear equality constraints as a separate Matrix (ceqg of size m2 X n or as an empty) where m2 & m3 are number of non-linear inequality and equality constraints respectively.
  • Default Values : options = list("MaxIter", [3000], "CpuTime", [600]);

The objective function must have header : 

F = fun(x)
where x is a n x 1 matrix of doubles and F is a m x 1 matrix of doubles where m is the total number of objective functions inside F. On input, the variable x contains the current point and, on output, the variable F must contain the objective function values.

By default, the gradient options for fminimax are turned off and and fmincon does the gradient opproximation of minmaxObjfun. In case the GradObj option is off and GradConstr option is on, fminimax approximates minmaxObjfun gradient using numderivative toolbox.

If we can provide exact gradients, we should do so since it improves the convergence speed of the optimization algorithm.

Furthermore, we must enable the "GradObj" option with the statement : 

minimaxOptions = list("GradObj",fGrad);
This will let fminimax know that the exact gradient of the objective function is known, so that it can change the calling sequence to the objective function. Note that, fGrad should be mentioned in the form of N x n where n is the number of variables, N is the number of functions in objective function.

The constraint function must have header : 

[c, ceq] = confun(x)
where x is a n x 1 matrix of dominmaxUbles, c is a 1 x nni matrix of doubles and ceq is a 1 x nne matrix of doubles (nni : number of nonlinear inequality constraints, nne : number of nonlinear equality constraints). On input, the variable x contains the current point and, on output, the variable c must contain the nonlinear inequality constraints and ceq must contain the nonlinear equality constraints.

By default, the gradient options for fminimax are turned off and and fmincon does the gradient opproximation of confun. In case the GradObj option is on and GradCons option is off, fminimax approximates confun gradient using numderivative toolbox.

If we can provide exact gradients, we should do so since it improves the convergence speed of the optimization algorithm.

Furthermore, we must enable the "GradCon" option with the statement : 

minimaxOptions = list("GradCon",confunGrad);
This will let fminimax know that the exact gradient of the objective function is known, so that it can change the calling sequence to the objective function.

The constraint derivative function must have header : 

[dc,dceq] = confungrad(x)
where dc is a nni x n matrix of doubles and dceq is a nne x n matrix of doubles.

The exitflag allows to know the status of the optimization which is given back by Ipopt.

  • exitflag=0 : Optimal Solution Found
  • exitflag=1 : Maximum Number of Iterations Exceeded. Output may not be optimal.
  • exitflag=2 : Maximum amount of CPU Time exceeded. Output may not be optimal.
  • exitflag=3 : Stop at Tiny Step.
  • exitflag=4 : Solved To Acceptable Level.
  • exitflag=5 : Converged to a point of local infeasibility.

For more details on exitflag see the ipopt documentation, go to http://www.coin-or.org/Ipopt/documentation/

The output data structure contains detailed informations about the optimization process. It has type "struct" and contains the following fields.

  • output.Iterations: The number of iterations performed during the search
  • output.Cpu_Time: The total cpu-time spend during the search
  • output.Objective_Evaluation: The number of Objective Evaluations performed during the search
  • output.Dual_Infeasibility: The Dual Infeasiblity of the final soution

The lambda data structure contains the Lagrange multipliers at the end of optimization. In the current version the values are returned only when the the solution is optimal. It has type "struct" and contains the following fields.

  • lambda.lower: The Lagrange multipliers for the lower bound constraints.
  • lambda.upper: The Lagrange multipliers for the upper bound constraints.
  • lambda.eqlin: The Lagrange multipliers for the linear equality constraints.
  • lambda.ineqlin: The Lagrange multipliers for the linear inequality constraints.
  • lambda.eqnonlin: The Lagrange multipliers for the non-linear equality constraints.
  • lambda.ineqnonlin: The Lagrange multipliers for the non-linear inequality constraints.

Examples

// A basic case :
// we provide only the objective function and the nonlinear constraint
// function
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;     //Objectives
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// The initial guess
x0 = [0.1,0.1];
// The expected solution : only 4 digits are guaranteed
xopt = [4 4]
fopt = [0 -64 -2 -8 0]
maxfopt = 0
// Run fminimax
[x,fval,maxfval,exitflag,output,lambda] = fminimax(myfun, x0)
// Press ENTER to continue

Examples

// A case where we provide the gradient of the objective
// functions and the Jacobian matrix of the constraints.
// The objective function and its gradient
function f=myfun(x)
f(1)= 2*x(1)^2 + x(2)^2 - 48*x(1) - 40*x(2) + 304;
f(2)= -x(1)^2 - 3*x(2)^2;
f(3)= x(1) + 3*x(2) -18;
f(4)= -x(1) - x(2);
f(5)= x(1) + x(2) - 8;
endfunction
// Defining gradient of myfun
function G=myfungrad(x)
G = [ 4*x(1) - 48, -2*x(1), 1, -1, 1;
2*x(2) - 40, -6*x(2), 3, -1, 1; ]'
endfunction
// The nonlinear constraints and the Jacobian
// matrix of the constraints
function [c, ceq]=confun(x)
// Inequality constraints
c = [1.5 + x(1)*x(2) - x(1) - x(2), -x(1)*x(2) - 10]
// No nonlinear equality constraints
ceq=[]
endfunction
// Defining gradient of confungrad
function [DC, DCeq]=cgrad(x)
// DC(:,i) = gradient of the i-th constraint
// DC = [
//   Dc1/Dx1  Dc1/Dx2
//   Dc2/Dx1  Dc2/Dx2
//   ]
DC= [
x(2)-1, -x(2)
x(1)-1, -x(1)
]'
DCeq = []'
endfunction
// Test with both gradient of objective and gradient of constraints
minimaxOptions = list("GradObj",myfungrad,"GradCon",cgrad);
// The initial guess
x0 = [0,10];
// The expected solution : only 4 digits are guaranteed
xopt = [0.92791 7.93551]
fopt = [6.73443  -189.778  6.73443  -8.86342  0.86342]
maxfopt = 6.73443
// Run fminimax
[x,fval,maxfval,exitflag,output] = fminimax(myfun,x0,[],[],[],[],[],[], confun, minimaxOptions)

Authors

  • Animesh Baranawal